Elementary divisors

In algebra, the elementary divisors of a module over a principal ideal domain (PID) occur in one form of the structure theorem for finitely generated modules over a principal ideal domain.

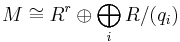
If $R$ is a PID and $M$ a finitely generated $R$ -module, then M is isomorphic to a unique sum of the form

$M\cong R^r\oplus \bigoplus_i R/(q_i)$

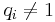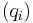where $q_i \neq 1$ and the $(q_i)$ are primary ideals.

The ideals 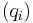$(q_i)$ are unique (up to order); the elements 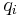$q_i$ are unique up to associatedness, and are called the elementary divisors. Note that in a PID, primary ideals are powers of primes, so the elementary divisors 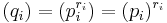$(q_i)=(p_i^{r_i}) = (p_i)^{r_i}$ . The nonnegative integer $r$ is called the free rank or Betti number of the module $M$ .

The elementary divisors of a matrix over a PID occur in the Smith normal form and provide a means of computing the structure of a module from a set of generators and relations.

References

B. Hartley; T.O. Hawkes (1970). Rings, modules and linear algebra. Chapman and Hall. ISBN 0-412-09810-5. Chap.11, p.182.
Chap. III.7, p.153 of Lang, Serge (1993), Algebra (Third ed.), Reading, Mass.: Addison-Wesley Pub. Co., ISBN 978-0-201-55540-0

Elementary divisors

See also

References